#300 - My Original Genres
For my 300th post, I've put together a collection of example puzzles for all of my original puzzle genres. As I create more in the future, this post will get updated. I hope you enjoy!
1. Ovotovata (oh-VOH-toh-VAH-tuh)
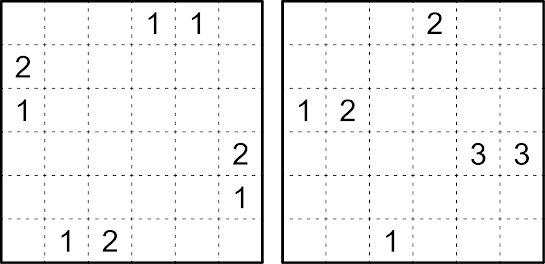
Draw a non-intersecting loop through the centers of some cells which visits each shaded region at least once. When the loop exits a clued region in any direction, it must travel in a straight line for exactly the indicated number of cells (turning on the Nth cell, where N is the value of the clue).
2. Aqre (AY-kurr)
Shade some cells so that all shaded cells form one orthogonally connected area. Regions with numbers must contain the indicated amount of shaded cells. There may not exist a run of more than three consecutive shaded or unshaded cells horizontally or vertically anywhere in the grid.
3. Pomoro (poh-MOH-roh)
Divide the grid into regions of orthogonally connected cells, each containing exactly one circle. A clue in a circle indicates the number of cells in its region. Numbers represent the amount of region borders that appear in a straight line in the indicated direction. Borders must separate two different regions. The edge of the grid does not count as a border.
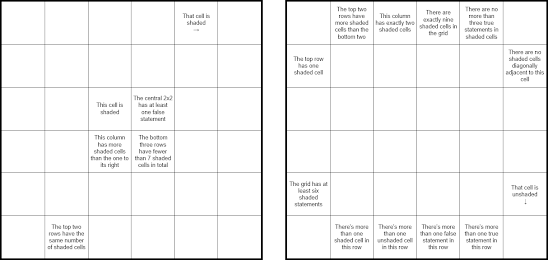
4. Grid Logic
Shade some cells so that no two shaded cells are orthogonally adjacent and the remaining unshaded cells form one orthogonally connected area. If a cell with a statement in it is unshaded, the statement must be true. If a cell with a statement in it is shaded, the statement may or may not be true.
An interactive solving interface is not available for these puzzles.
Click on the image for higher resolution.
5. Tetraview
Shade some tetrominoes of cells so that no two tetrominoes touch each other orthogonally. Clued cells cannot be shaded, and a clue means that the first tetromino seen in a straight line in the indicated direction is of the shape associated with that letter.
6. Pointer Loop
Divide the grid into dominoes and place a two-cell-long arrow in each one. The dominoes must all form a single continuous loop, where each domino’s arrow points to the next.
7. Voxas (VAHK-sis)
Divide the grid into 1x2 and 1x3 regions. Borders must separate two different regions. Borders with white dots separate regions with the same size and orientation. Borders with black dots separate regions with neither the same size nor the same orientation. Borders with grey dots separate regions with either the same size or the same orientation, but not both.
8. Zabajaba (ZA-buh-JA-buh)
Locate some blocks in the grid, each of which are either 1x3 or 2x2, which may not overlap each other. All of the blocks must form one orthogonally connected area, but two blocks of the same shape and orientation may not share an edge. Clued cells cannot be used by blocks and indicate the number of blocks located at least partially in the (up to) eight cells surrounding the clue.
9. U-Turns
Draw a non-intersecting path through the centers of some cells which passes through every white circle and no black circles. Grey circles mark the ends of the path. Between each pair of circles the path uses, the path must turn exactly twice, and both turns must be in the same direction.
10. Eels
Shade some cells such that each orthogonally connected group of shaded cells or unshaded cells forms a one-wide path that may not touch itself orthogonally and is at least four cells in length. Clued cells cannot be shaded. A black arrow means that the adjacent cell in the indicated direction is shaded. A white arrow means that the adjacent cell in the indicated direction is unshaded. A number in a circle indicates the amount of cells in the path the circle belongs to.
11. Disorderly Loop
Draw a non-intersecting loop through the centers of some cells. Clued cells may not be used by the loop. Clues represent the lengths of the next N line segments appearing in the loop, not necessarily in order, starting with a line in the cell adjacent to the clue in the direction of its arrow and moving in the direction of the arrow, where N is the amount of numbers in the clue.
12. Yoque (YOHK)
Connect some pairs of orthogonally adjacent dots to form paths connecting pairs of circles. Each path must turn exactly once, and each path must be crossed exactly once by another path. Two perpendicular line segments may intersect each other, but not turn or stop at their intersection or otherwise overlap. Two circles containing the same letter must be ends of the same path. Two circles containing different letters may not.
13. Square Jam
Divide the grid into square regions of orthogonally connected cells. A number indicates the side length of the square it’s in. Region borders may not form any four-way intersections.
14. Vagabond
Draw a non-intersecting loop through the centers of all unshaded cells. No two adjacent regions may be visited by the loop the same number of times. A number in a region indicates how many times it’s visited by the loop.
15. Ant Mill
Shade some dominoes of cells. No two dominoes may touch orthogonally, but each domino must touch exactly two others by the corners such that all dominoes form a single loop. Cells separated by a square must both be shaded or both be unshaded. Cells separated by an X must not.
16. Xerophile
Shade some cells to form a non-intersecting loop which does not touch itself orthogonally. Every cell which is orthogonally adjacent to exactly one shaded cell is marked with a circle.


















What a treat! I've solved an Ovotovata and a Pomoro and I'll definitely try all of them when I have the time. Didn't even know you invented Aqre! How cool is that ?!
ReplyDeleteAnyways, here's to the next 300 :D
Lovely, thanks! I hope you enjoy the rest as well :D
DeleteDone with Ovatavata .. Is it a requirement in these type of puzzles that in non-clued shaded regions, loop needs to travel exactly N number of cells before turning ?
ReplyDeleteAqre too done.
DeleteIt's not. However, a region (shaded or not) with a question mark in it must.
Delete